问题描述
LeetCode 1111. 有效括号的嵌套深度 (opens in a new tab),难度中等。
有效括号字符串 定义:对于每个左括号,都能找到与之对应的右括号,反之亦然。详情参见题末「有效括号字符串」部分。
嵌套深度 depth 定义:即有效括号字符串嵌套的层数,depth(A) 表示有效括号字符串 A 的嵌套深度。详情参见题末「嵌套深度」部分。
有效括号字符串类型与对应的嵌套深度计算方法如下图所示:
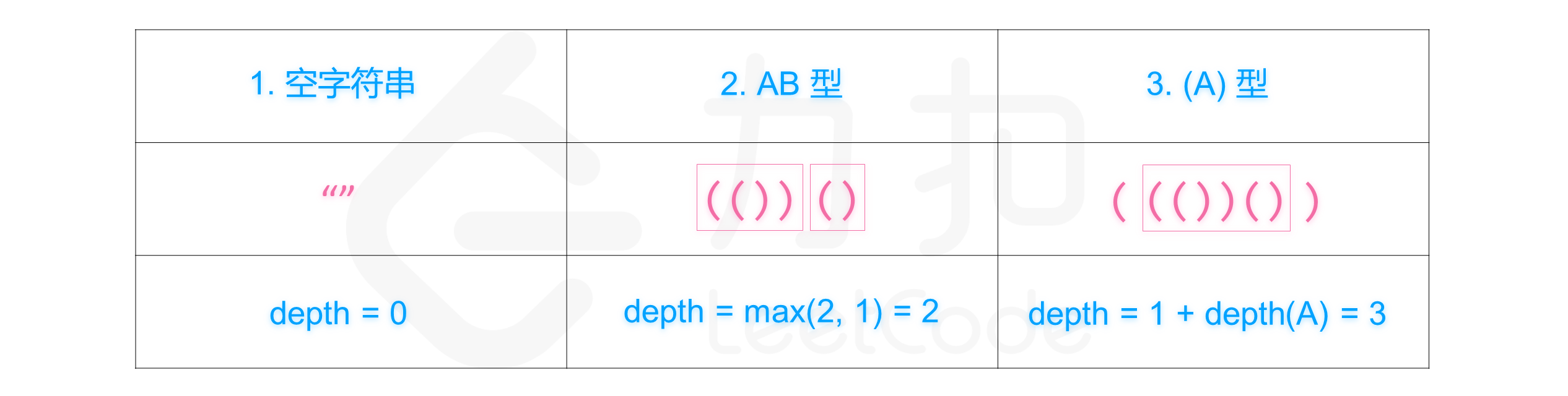
给你一个「有效括号字符串」 seq,请你将其分成两个不相交的有效括号字符串,A 和 B,并使这两个字符串的深度最小。
- 不相交:每个
seq[i]只能分给A和B二者中的一个,不能既属于A也属于B。 A或B中的元素在原字符串中可以不连续。A.length + B.length = seq.length- 深度最小:
max(depth(A), depth(B))的可能取值最小。
划分方案用一个长度为 seq.length 的答案数组 answer 表示,编码规则如下:
answer[i] = 0,seq[i]分给A。answer[i] = 1,seq[i]分给B。
如果存在多个满足要求的答案,只需返回其中任意 一个 即可。
示例 1
输入:seq = "(()())" 输出:[0,1,1,1,1,0]
示例 2
输入:seq = "()(())()" 输出:[0,0,0,1,1,0,1,1] 解释:本示例答案不唯一。 按此输出 A = "()()", B = "()()", max(depth(A), depth(B)) = 1,它们的深度最小。 像 [1,1,1,0,0,1,1,1],也是正确结果,其中 A = "()()()", B = "()", max(depth(A), depth(B)) = 1 。
提示:
1 < seq.size <= 10000
有效括号字符串:
仅由 "(" 和 ")" 构成的字符串,对于每个左括号,都能找到与之对应的右括号,反之亦然。
下述几种情况同样属于有效括号字符串:
1. 空字符串
2. 连接,可以记作 AB(A 与 B 连接),其中 A 和 B 都是有效括号字符串
3. 嵌套,可以记作 (A),其中 A 是有效括号字符串嵌套深度:
类似地,我们可以定义任意有效括号字符串 s 的 嵌套深度 depth(S):
1. s 为空时,depth("") = 0
2. s 为 A 与 B 连接时,depth(A + B) = max(depth(A), depth(B)),其中 A 和 B 都是有效括号字符串
3. s 为嵌套情况,depth("(" + A + ")") = 1 + depth(A),其中 A 是有效括号字符串
例如:"","()()",和 "()(()())" 都是有效括号字符串,嵌套深度分别为 0,1,2,而 ")(" 和 "(()" 都不是有效括号字符串。题解
基于索引的奇偶性来分配左右括号
-
遍历输入字符串
seq中的每个字符。 -
对于每一个左括号
(,根据其索引i的奇偶性将其分配给结果数组result。如果i是奇数,则result[i] = 1;如果i是偶数,则result[i] = 0。 -
对于每一个右括号
),采用类似的逻辑,但是注意这里是根据i + 1的奇偶性来分配。这意味着如果一个右括号的索引为偶数,它就被分配到奇数组(因为i + 1为奇数),反之亦然。
为什么这样能保证右括号可以与一个左括号匹配呢?关键在于序列的有效性和索引的奇偶性分配策略。
-
序列有效性保证匹配:由于输入的括号序列是有效的,这意味着对于每个右括号,都有一个相匹配的左括号存在。因此,主要问题不在于是否能够找到匹配的左括号,而在于如何分配这些匹配以减小最大深度。
-
奇偶分配实现平衡:通过将相邻的括号分配到不同的组中(即一个左括号和紧随其后的右括号不会被分到同一组),我们实际上是在减少任何单一组内的嵌套深度。考虑到左右括号的总数是相等的,这种分配方法不仅保证了每个组都是有效的括号序列,而且还帮助平衡了两个组的深度。
-
交替分配避免深度增加:通过奇偶分配,我们确保了不会有连续的左括号或右括号分配到同一组,这减少了连续括号导致的深度增加。例如,对于连续的左括号
((,按照奇偶分配,它们会被分到不同的组,从而避免了在任一组中形成过深的嵌套。
class Solution {
public int[] maxDepthAfterSplit(String seq) {
int[] result = new int[seq.length()];
for (int i = 0; i < seq.length(); ++i) {
if (seq.charAt(i) == '(') {
result[i] = i & 1;
} else {
result[i] = (i + 1) & 1;
}
}
return result;
}
}