问题描述
LeetCode 100334. 包含所有 1 的最小矩形面积 I (opens in a new tab),难度中等。
给你一个二维 二进制 数组 grid。请你找出一个边在水平方向和竖直方向上、面积 最小 的矩形,并且满足 grid 中所有的 1 都在矩形的内部。
返回这个矩形可能的 最小 面积。
示例 1
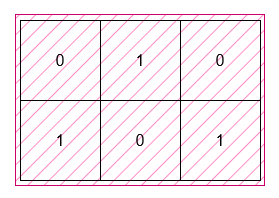
输入: grid = [[0,1,0],[1,0,1]] 输出: 6 解释: 这个最小矩形的高度为 2,宽度为 3,因此面积为 2 * 3 = 6。
示例 2
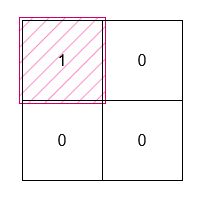
输入: grid = [[0,0],[1,0]] 输出: 1 解释: 这个最小矩形的高度和宽度都是 1,因此面积为 1 * 1 = 1。
提示:
1 <= grid.length, grid[i].length <= 1000grid[i][j]是 0 或 1。- 输入保证
grid中至少有一个 1 。
题解
遍历
解题思路:去掉矩形上下左右全为 0 的行和列
Solution.java
class Solution {
public int minimumArea(int[][] grid) {
int row = grid.length;
int col = grid[0].length;
int minRow = row; // 最小行数
int minCol = col; // 最小列数
// 从上往下判断行是否都为 0,如果整行都为 0,minRow--
// 反之停止循环
boolean flag = true;
for (int r = 0; r < row; ++r) {
for (int c = 0; c < col; ++c) {
if (grid[r][c] == 1) {
flag = false;
break;
}
}
if (!flag) break;
minRow--;
}
// 从下往上判断行是否都为 0
flag = true;
for (int r = row - 1; r > 0; --r) {
for (int c = 0; c < col; ++c) {
if (grid[r][c] == 1) {
flag = false;
break;
}
}
if (!flag) break;
minRow--;
}
// 从左往右判断列是否都为 0
flag = true;
for (int c = 0; c < col; ++c) {
for (int r = 0; r < row; ++r) {
if (grid[r][c] == 1) {
flag = false;
break;
}
}
if (!flag) break;
minCol--;
}
// 从右往左判断列是否都为 0
flag = true;
for (int c = col - 1; c > 0; --c) {
for (int r = 0; r < row; ++r) {
if (grid[r][c] == 1) {
flag = false;
break;
}
}
if (!flag) break;
minCol--;
}
return minCol * minRow;
}
}